1. 特征选择
1.1 熵与条件熵
1.熵
熵是表示随机变量不确定性的度量。设XXX是一个取有限个值的离散随机变量，其概率分布为

pi=P(X=xi),i=1,2,...,n(1)p_i = P(X=x_i), i=1,2,...,n \tag{1}
p 
i

 =P(X=x 
i

 ),i=1,2,...,n(1)

则随机变量XXX的熵定义为：

H(X)=−∑ni=1pilogpi(2)H(X) = -\sum_{i=1}^n p_i \log p_i \tag{2}
H(X)=− 
i=1
∑
n

 p 
i

 logp 
i

 (2)

上式也可以写作：

H(p)=−∑ni=1pilogpi(3)H(p) = -\sum_{i=1}^n p_i \log p_i \tag{3}
H(p)=− 
i=1
∑
n

 p 
i

 logp 
i

 (3)

熵也可以这样理解：
随机变量的联合概率：∏ni=1pi\prod_{i=1}^n p_i∏ 
i=1
n

 p 
i

 
其负对数：−∑ni=1logpi-\sum_{i=1}^n \log p_i−∑ 
i=1
n

 logp 
i

 
其负对数的期望： −∑ni=1pilogpi-\sum_{i=1}^n p_i \log p_i−∑ 
i=1
n

 p 
i

 logp 
i

 

当随机变量只取两个值，例如1,0时，熵为：

H(p)=−plogp−(1−p)log(1−p)(4)H(p) = -p \log p - (1-p) \log (1-p) \tag{4}
H(p)=−plogp−(1−p)log(1−p)(4)

用Python画出两个变量的概率和熵的图像：

def plot_entropy():
    """
    H(p) = -p log p - (1-p)log(1-p)
    :return:
    """
    p = range(1, 1000)
    p = [i/1000 for i in p]
    H_p_e = [(-i * np.log(i) - (1-i) * np.log(1-i)) for i in p]
    H_p_2 = [(-i * np.log2(i) - (1-i) * np.log2(1-i)) for i in p]
    H_p_10 = [(-i * np.log10(i) - (1 - i) * np.log10(1 - i)) for i in p]
    # 画图
    fig, ax = plt.subplots()
    ax.plot(p, H_p_e, c='red', label='H(P) log_e')
    ax.plot(p, H_p_2, c='blue', label='H(P) log_2')
    ax.plot(p, H_p_10, c='green', label='H(P) log_10')
    ax.legend()
    plt.show()

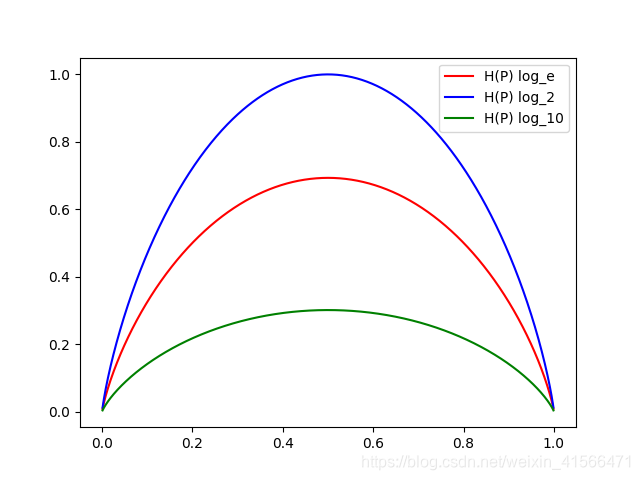
从图中可以看出当p=0p=0p=0和p=1p=1p=1时，H(p)=0H(p) = 0H(p)=0,此时随机变量完全确定，当p=0.5p=0.5p=0.5时,此时熵取得最大值，随机变量的不确定性最大。不仅仅是两个变量，当多变量时，随机变量越不确定，其熵也就越大。

思考：
1.取log\loglog底数到底是多少?
2.这种形状很像抛物线，如果用抛物线的函数量化信息是不是也可以？

2.条件熵

设有随机变量(X,Y)(X,Y)(X,Y)，其联合概率分布为：

pij=P(X=xi,Y=yj),i=1,2,...,n;j=1,2,...mp_{ij} = P(X=x_i, Y=y_j), i=1,2,...,n; j=1,2,...m
p 
ij

 =P(X=x 
i

 ,Y=y 
j

 ),i=1,2,...,n;j=1,2,...m

条件熵：

H(Y∣X)=∑n(i=1)piH(Y∣X=xi)H(Y|X) = \sum_{(i=1)}^n p_i H(Y|X=x_i)
H(Y∣X)= 
(i=1)
∑
n

 p 
i

 H(Y∣X=x 
i

 )

表示在已知随机变量XXX的条件下随机变量YYY的不确定性。

1.2 信息增益
一般地，熵H(Y)H(Y)H(Y)与条件熵H(Y∣X)H(Y|X)H(Y∣X)只差为互信息。决策树学习中的信息增益等价于训练数据集中类与特征的互信息。
信息增益：

g(Y,X)=H(Y)−H(Y∣X)g(Y,X) = H(Y) - H(Y|X)
g(Y,X)=H(Y)−H(Y∣X)

在决策树中可以这样理解：首先有标签信息，其不确定性表示为H(Y)H(Y)H(Y)，当加入一部分特征数据XXX后，在有特征的情况下，标签的不确定性表示为H(Y∣X)H(Y|X)H(Y∣X)，其不确定性一定会降低，那么降低的程度量化表示就是g(Y,X)g(Y,X)g(Y,X)。g(Y,X)g(Y,X)g(Y,X)越大，表示提供的XXX对YYY的确定性影响越大，也就表示XXX特征越有效。

信息增益和后面信息增益比就是筛选特征有效性的方法，在特征工程中可以直接应用。

1.3 基尼指数
分类问题中，假设有KKK个类，样本点属于第kkk类的概率为pkp_kp 
k

 ，则概率分布的基尼指数定义为：

Gini(p)=∑Kk=1pk(1−pk)=∑Kk=1pk−∑Kk=1p2k=1−∑Kk=1p2kGini(p) = \sum_{k=1}^K p_k(1-p_k) = \sum_{k=1}^K p_k - \sum_{k=1}^K p_k^2 = 1 - \sum_{k=1}^K p_k^2
Gini(p)= 
k=1
∑
K

 p 
k

 (1−p 
k

 )= 
k=1
∑
K

 p 
k

 − 
k=1
∑
K

 p 
k
2

 =1− 
k=1
∑
K

 p 
k
2

 

对于二分类问题p1+p2=1,p1=p,p2=1−pp_1 + p_2 = 1, p_1 = p, p_2 = 1 - pp 
1

 +p 
2

 =1,p 
1

 =p,p 
2

 =1−p：

Gini(p)=1−∑2k=1p2k=1−p21−p22=1−p2−(1−p)2=2p−p2Gini(p) = 1 - \sum_{k=1}^2 p_k^2 = 1 - p_1^2 - p_2^2 = 1 - p^2 - (1-p)^2 = 2p-p^2
Gini(p)=1− 
k=1
∑
2

 p 
k
2

 =1−p 
1
2

 −p 
2
2

 =1−p 
2
 −(1−p) 
2
 =2p−p 
2
 



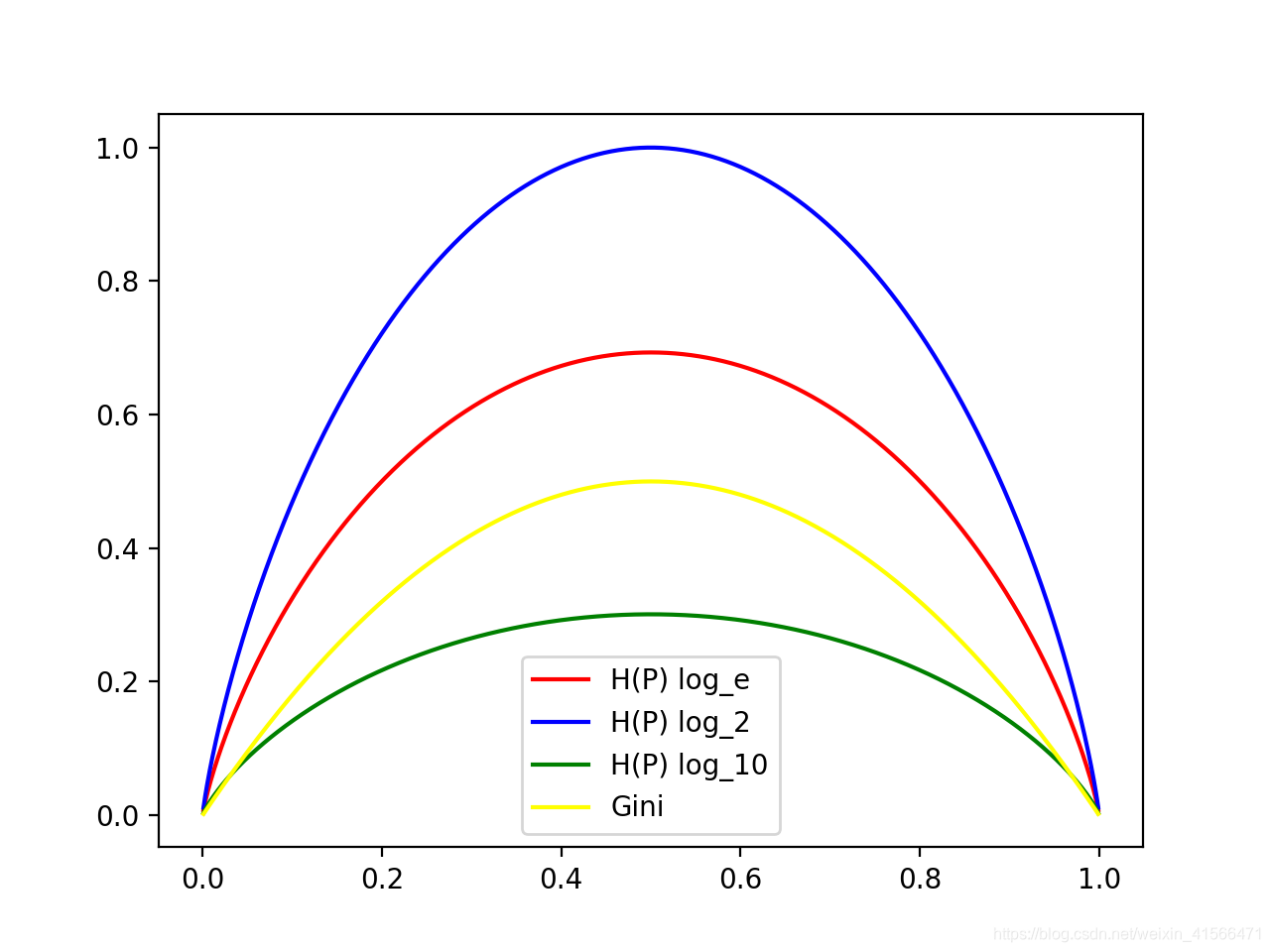
1.5 最小二乘回归树
给你训练集：

D={(x1,y,),(x2,y2),...,(xN,yN)}D = \{ (x_1, y_,), (x_2, y_2), ..., (x_N, y_N) \}
D={(x 
1

 ,y 
,

 ),(x 
2

 ,y 
2

 ),...,(x 
N

 ,y 
N

 )}

假设将空间划分为MMM个单元R1,R2,...,RMR_1, R_2, ..., R_MR 
1

 ,R 
2

 ,...,R 
M

 ，并且在每一个单元上有一个固定的输出值cmc_mc 
m

 ，于是回归树模型可以表示为：

f(x)=∑Mm=1cmI(x∈Rm)f(x) = \sum_{m=1}^M c_mI(x \in R_m)
f(x)= 
m=1
∑
M

 c 
m

 I(x∈R 
m

 )

其中：

cm=ave(yi∣xi∈Rm)c_m = ave (y_i | x_i \in R_m)
c 
m

 =ave(y 
i

 ∣x 
i

 ∈R 
m

 )

当输入空间划分确定式，可以用平方误差来表示回归树对训练数据的预测误差：

∑xi∈Rm(yi−f(xi))2\sum_{x_i \in R_m} (y_i - f(x_i))^2
x 
i

 ∈R 
m

 
∑

 (y 
i

 −f(x 
i

 )) 
2
 

在回归树模型中，对空间的划分采用启发式的方法，选择第jjj个变量x(j)x^{(j)}x 
(j)
 和它的取值sss,分别作为切分变量和切分点，并定义两个区域：

R1(j,s)={x∣x(j)≤s},R2j,s={x∣x(j)>s}R_1(j,s) = \{ x|x^{(j)} \le s \}, R_2{j,s} = \{x|x^{(j)} > s \}
R 
1

 (j,s)={x∣x 
(j)
 ≤s},R 
2

 j,s={x∣x 
(j)
 >s}

然后寻找最优切分变量jjj于切分点sss ：

minj,s[minc1∑xi∈R1(j,s)(yi−c1)2+minc2∑xi∈R2(j,s)(yi−c2)2]\min_{j,s} [\min_{c_1} \sum_{x_i \in R_1(j,s)} (y_i - c_1)^2 + \min_{c_2} \sum_{x_i \in R_2(j,s)} (y_i - c_2)^2 ]
j,s
min

 [ 
c 
1

 
min

  
x 
i

 ∈R 
1

 (j,s)
∑

 (y 
i

 −c 
1

 ) 
2
 + 
c 
2

 
min

  
x 
i

 ∈R 
2

 (j,s)
∑

 (y 
i

 −c 
2

 ) 
2
 ]

对固定的输入变量jjj可以找到最优的切分点sss:

cˆ1=ave(yi∣xi∈R1(j,s)),cˆ2=ave(yi∣xi∈R2(j,s))\hat c_1 = ave (y_i|x_i \in R_1(j,s)), \hat c_2 = ave(y_i|x_i \in R_2(j,s))
c
^
  

 =ave(y 
i

 ∣x 
i

 ∈R 

 (j,s)), 
c
^
  

 =ave(y 
i

 ∣x 
i

 ∈R 

 (j,s))

这样就可以将空间划分为两个区域，接下来，重复划分过程，直到满足停止条件。

2. python实现决策树
2.1 模型实现
import numpy as np
import pandas as pd
from copy import deepcopy


class MyDecisionTree(object):
    def __init__(self, max_depth=10, criterion="entropy"):
        """
        CART 分类回归树的实现
        :param max_depth: 树的最大深度，默认值是10
        :param criterion: {'mse', 'entropy', 'gini'}
            'mse': 均方误差计算，用来实现回归树
            'entropy': 用信息增益来筛选特征
            'gini'：用gini系数来筛选特征
        :param dispersed: 是否是离散值。离散值和连续值在进行特征分箱处理时不是一样的
        :param label_map: 可以将标签的字符串映射成为数字，便于计算信息增益
        :param tree: 最后的结果，字典存储
        """

        self.max_depth = max_depth
        self.criterion = criterion
       
        self.dispersed = None
        self.label_map = None
        self.tree = None
        self.eps = np.finfo(np.float32).eps

    def _entropy(self, y):
        """
        计算熵
        H(x) = - sum p_i* log p_i
        :param y: 标签值
        :return:
        """

        hist = np.bincount(y)
        ps = hist / np.sum(hist)
        return 1 - np.sum(np.power(ps + self.eps, 2))

    def _gini(self, y):
        """
        计算Gini
        G(p) = 1 - sum p^2
        :param y:
        :return:
        """
        hist = np.bincount(y)
        ps = hist / np.sum(hist)
        return 1 - np.sum(np.power(ps, 2))

    def _mse(self, y):
        """
        计算均方误差
        :param y:
        :return:
        """
        return np.mean(np.power((y - np.mean(y)),2))

    def _get_loss(self, df_data, df_sub_data_1, df_sub_data_2):
        """
        计算信息增益
        :param df_data: 样本
        :param df_sub_data_1: 样本分裂后的第一部分样本
        :param df_sub_data_2: 样本分裂后的第二部分样本
        :return:
        """
        if self.criterion == "entropy":
            loss = self._entropy
        elif self.criterion == "gini":
            loss = self._gini
        elif self.criterion == "mse":
            loss = self._mse
        else:
            raise TabError('wrong criterion.')

        parent_len = len(df_data)
        sub_1_len = len(df_sub_data_1)
        sub_2_len = len(df_sub_data_2)

        if parent_len <= 0 or sub_1_len <= 0 or sub_2_len <= 0:
            return 0

        parent_y = df_data['label'].values
        if isinstance(parent_y[0], str):
            parent_y = np.array([self.label_map[y] for y in parent_y])
        parent_y = np.array(parent_y, dtype=int)

        parent_loss = loss(parent_y)

        sub_1_y = df_sub_data_1['label'].values
        if isinstance(sub_1_y[0], str):
            sub_1_y = np.array([self.label_map[y] for y in sub_1_y])
        sub_1_y = np.array(sub_1_y, dtype=int)
        sub_1_loss = loss(sub_1_y)


        sub_2_y = df_sub_data_2['label'].values
        if isinstance(sub_2_y[0], str):
            sub_2_y = np.array([self.label_map[y] for y in sub_2_y])
        sub_2_y = np.array(sub_2_y, dtype=int)
        sub_2_loss = loss(sub_2_y)

        child_loss = (sub_1_len / parent_len) * sub_1_loss + (sub_2_len / parent_len) * sub_2_loss
        return parent_loss - child_loss


    def _choose_best_feature(self, df_data):
        """
        遍历所有的特征，之后遍历该特征的所有值，选出信息增益最大的特征和对应的值
        :param df_data:
        :return:
        """
        columns = list(df_data.columns)
        if 'label' in columns:
            columns.remove('label')

        best_gain = -np.inf
        best_feature = None
        best_value = None
        for column in columns:
            values = df_data[column].unique()
            for value in values:
                # 这儿进行分组的时候，离散变量和连续变量是不一样的
                if column in self.dispersed:
                    df_sub_data_1 = df_data[df_data[column] == value]
                    df_sub_data_2 = df_data[df_data[column] != value]
                else:
                    if value == max(values):
                        continue
                    df_sub_data_1 = df_data[df_data[column] <= value]
                    df_sub_data_2 = df_data[df_data[column] > value]
                gain = self._get_loss(df_data, df_sub_data_1, df_sub_data_2)
                if best_gain < gain:
                    best_gain = gain
                    best_feature = column
                    best_value = value
        return best_feature, best_value


    def _create_tree(self, df_data, depth=0):
        """
        创建决策树
        :param df_data:
        :param depth: 决策树的深度
        :return:
        """
        y = df_data['label'].values

        # 终止条件一：所有样本都属于同一类
        if len(set(y)) <= 1:
            return y[0]

        # 终止条件二：虽然样本不属于同一类，但是特征值为空，这种情况只能取数目多的那一类
        # 终止条件三：树的深度达到了限制条件
        if (len(df_data.iloc[0]) <= 1) or (depth>=self.max_depth):
            if self.criterion != 'mse':
                y_dict = {}
                for y_s in y:
                    if y_s in y_dict.keys():
                        y_dict[y_s] += 1
                    else:
                        y_dict[y_s] = 1

                best_y = None
                count_y = 0
                for key, value in y_dict.items():
                    if count_y < value:
                        count_y = value
                        best_y = key
                return best_y
            else:
                return np.average(y)

        depth += 1

        # 选择最优的切分点
        best_feature, best_value = self._choose_best_feature(df_data)

        if best_feature in self.dispersed:
            df_sub_data_1 = df_data[df_data[best_feature] == best_value]
            df_sub_data_2 = df_data[df_data[best_feature] != best_value]

        else:
            df_sub_data_1 = df_data[df_data[best_feature] <= best_value]
            df_sub_data_2 = df_data[df_data[best_feature] > best_value]
        tree = {best_feature: {'threshold': best_value}}

        if len(df_sub_data_1[best_feature].unique()) <= 0:
            del df_sub_data_1[best_feature]
        if len(df_sub_data_2[best_feature].unique()) <= 0:
            del df_sub_data_2[best_feature]

        tree[best_feature][str(best_value)] = self._create_tree(df_sub_data_1, depth)
        tree[best_feature]['not_' + str(best_value)] = self._create_tree(df_sub_data_2, depth)

        return tree

    def fit(self, data_set, columns, dispersed=list(), label_map=None):
        """
        模型训练的入口
        :param data_set: 输入的训练数据集
        :param columns: 样本的特征名称
        :param dispersed: 离散特征的名称
        :param label_map: 标签的映射
        :return:
        """
        self.dispersed = dispersed
        self.label_map = label_map
        self.columns = columns
        if 'label' not in columns:
            columns.append('label')
        df_data = pd.DataFrame(data_set, columns=columns)


        self.tree = self._create_tree(df_data)

    def predict(self, X, columns):
        """
        预测结果
        :param X: 输入数据
        :param columns:
        :return:
        """
        df_data = pd.DataFrame(X, columns=columns)
        result_list = []
        for i in range(len(df_data)):
            ret_df_data = df_data.iloc[i]
            result = self._predict_one(ret_df_data, deepcopy(self.tree))
            result_list.append(result)

        return result_list

    def _predict_one(self, df_data, tree_dict):
        if isinstance(tree_dict, int) or isinstance(tree_dict, str) or isinstance(tree_dict, np.float):
            return tree_dict
        key = list(tree_dict.keys())[0]
        value = df_data[key]
        threshold = tree_dict[key]['threshold']

        if key in self.dispersed:
            if value == threshold:
                value = str(threshold)
            else:
                value = 'not_' + str(threshold)
        else:
            if value <= threshold:
                value = str(threshold)
            else:
                value = 'not_' + str(threshold)
        return self._predict_one(df_data, tree_dict[key][value])


2.2 模型测试一
def run_my_model():
    data_set = [['youth', 'no', 'no', 1, 'refuse'],
                ['youth', 'no', 'no', 2, 'refuse'],
                ['youth', 'yes', 'no', 2, 'agree'],
                ['youth', 'yes', 'yes', 1, 'agree'],
                ['youth', 'no', 'no', 1, 'refuse'],
                ['mid', 'no', 'no', 1, 'refuse'],
                ['mid', 'no', 'no', 2, 'refuse'],
                ['mid', 'yes', 'yes', 2, 'agree'],
                ['mid', 'no', 'yes', 3, 'agree'],
                ['mid', 'no', 'yes', 3, 'agree'],
                ['elder', 'no', 'yes', 3, 'agree'],
                ['elder', 'no', 'yes', 2, 'agree'],
                ['elder', 'yes', 'no', 2, 'agree'],
                ['elder', 'yes', 'no', 3, 'agree'],
                ['elder', 'no', 'no', 1, 'refuse']
                ]
    columns = ['age', 'working', 'house', 'credit_situation']
    my = MyDecisionTree()
    train_data_set = data_set[:12]
    test_data_set = data_set[12:]

    my.fit(train_data_set, columns, dispersed=['age', 'working', 'house'], label_map={'refuse':0, 'agree':1})                          
    print(my.tree)
    test_X = [i[:-1] for i in test_data_set]
    test_Y = [i[-1] for i in test_data_set]

    pred_Y = my.predict(test_X, columns=['age', 'working', 'house', 'credit_situation'])
    print('result: ')
    print('test: ', test_Y)
    print('pred: ', pred_Y)

结果：
result:
test: [‘agree’, ‘agree’, ‘refuse’]
pred: [‘agree’, ‘agree’, ‘refuse’]

2.3 模型测试二
def run_my_model_v2():
    from sklearn.datasets import load_iris
    from sklearn.model_selection import train_test_split
    iris_data = load_iris()
    print(iris_data)
    print(iris_data['data'])
    print(iris_data['target'])
    print(iris_data['target_names'])



    my = MyDecisionTree()
    df = pd.DataFrame(iris_data['data'], columns=['f1', 'f2', 'f3', 'f4'])
    df['label'] = iris_data['target']

    train_data, test_data = train_test_split(df)
    print('train_data:')
    print(train_data)

    my.fit(train_data.values, train_data.columns)
    print(my.tree)
    test_result = my.predict(test_data.values, test_data.columns)
    test = [int(y) for y in test_data['label'].values]
    pred = [int(y) for y in test_result]
    print('result:')
    print('test: ', test)
    print('pred: ', pred)

结果如下：
result:
test: [2, 0, 0, 0, 1, 1, 2, 2, 1, 2, 2, 0, 1, 0, 1, 0, 1, 2, 1, 0, 2, 0, 2, 0, 1, 1, 0, 2, 1, 2, 2, 2, 1, 1, 1, 2, 0, 0]
pred: [2, 0, 0, 0, 1, 1, 2, 2, 1, 2, 2, 0, 1, 0, 1, 0, 1, 2, 1, 0, 2, 0, 1, 0, 1, 1, 0, 2, 1, 2, 1, 2, 1, 1, 1, 2, 0, 0]